公害防止管理者の過去問|令和4年 大規模水質特論 問3 問題と解説
問題3
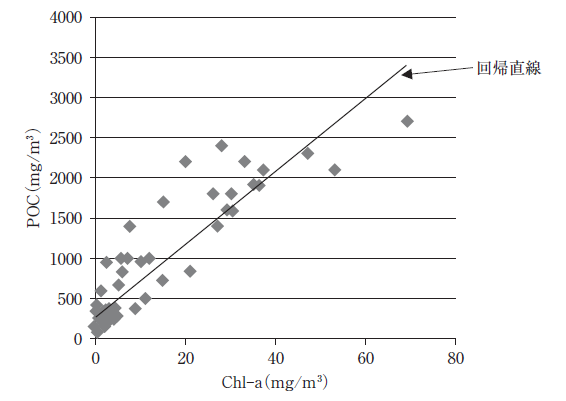
図はある沿岸域において得られているChl-a(クロロフィル-a濃度)とPOC(粒子状有機炭素量)との関係を示したものである。今、この水域の水中の植物プランクトン量がChl-aとして、60mg/m3であった。
この水域の植物プランクトン量に由来するCOD(mg/L)の推定値として最も近い値はどれか。
ただし、COD(mg/L)と植物プランクトンの炭素生物量(mg/m3)との比は1.5×10-3:1であるとする。また、計算には図中の回帰直線を用いるものとする。
- 0.15
- 0.41
- 0.80
- 1.5
- 4.1
問題3の解答
正解は「5」です。
問題3の解説
この問題は、図(回帰直線)を使って Chl-a → POC(粒子状有機炭素)→ COD と順番に換算していく 計算問題です。ポイントは、「図から読み取る量(POC)」と、「与えられた比で換算する量(COD)」を混同しないことです。
解答に至るまでのステップ
— ステップ1 回帰直線から Chl-a=60 mg/m³ に対応する POC を読み取る
このステップでは、図の回帰直線を使って Chl-a が 60 mg/m³ のときの POC(mg/m³)を推定します。
理由は、問題文が「計算には図中の回帰直線を用いる」と指定しているためで、散布点ではなく回帰直線上の値を採用する必要があるからです。
図の横軸 60 mg/m³ 付近から回帰直線をたどると、縦軸(POC)は およそ 3,000 mg/m³程度に読めます。ここでは代表値として、
- POC ≈ 3,000 mg/m³
と置きます(「最も近い値」を選ぶ問題なので、読み取りはこの程度の幅で十分に判断できます)。
— ステップ2 POC を「植物プランクトン由来の炭素生物量」として扱う
このステップでは、ステップ1で得た POC を、問題が求めている「植物プランクトン量に由来するCOD」を計算するための炭素量の代表値として用います。理由は、この図が Chl-a(植物プランクトン量の指標)と POC(粒子状有機炭素)の関係を示しており、回帰直線から得た POC を「植物プランクトン由来の炭素量」の推定値として用いる、という設問の意図になっているためです。
したがって、
- 植物プランクトンの炭素生物量(mg/m³) ≈ 3,000 mg/m³
と整理します。
— ステップ3 与えられた比を用いて COD(mg/L)に換算する
このステップでは、問題文で与えられている換算条件を、そのまま使って COD を求めます。理由は、問題文がすでに COD(mg/L)と炭素生物量(mg/m³)の比を与えており、ここで余計な単位換算(1 m³=1000 L など)を追加すると、二重に換算してしまう危険があるからです。
与えられた比は、
- COD(mg/L) : 炭素生物量(mg/m³) = 1.5×10⁻³ : 1
ですから、
COD≒ 1.5×10⁻³×3000=4.5
となります。
— ステップ4 選択肢の中で最も近い値を選ぶ
計算結果は 約 4.5 mg/L なので、選択肢では 4.1 mg/L が最も近い値です。したがって ⑤ が正解になります。
問題のポイント
この問題で迷いやすいのは、次の2点です。
- 回帰直線を使う
散布点にはばらつきがあるため、問題の指示どおり「回帰直線上の値」を採用します。読み取りに多少の幅があっても、最終的に近い選択肢を選ぶ設計になっています。 - 比(1.5×10⁻³ : 1)は“そのまま掛け算で使う”
ここで「mg/m³ と mg/L の換算を別に入れたくなる」ことがありますが、問題文はすでに COD(mg/L)と炭素生物量(mg/m³)の対応を比として与えています。したがって、余計な 1/1000 を足すと小さく見積もりすぎる原因になります。












コメント