公害防止管理者の過去問|令和5年 ばいじん・粉じん特論 問1 問題と解説
問題1
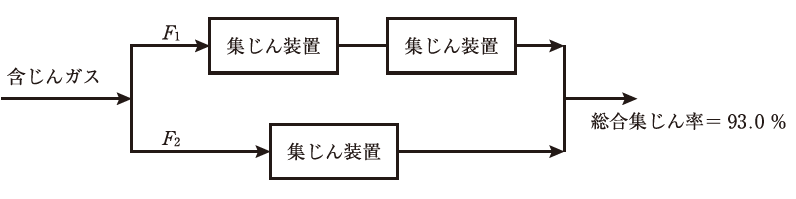
含じんガスを分割(流量比F1:F2=1:2)した後、同じ性能の集じん装置3基を図のように配置して集じんし、再びガスを合一したところ、総合集じん率が93.0%になった。
集じん装置単体の集じん率は何%か。
ただし、集じん率は集じん装置の設置位置によらず同一であるものとし、また、排ガスの分割によりばいじんも流量比に応じて分割されるものとする。
- 82
- 84
- 86
- 88
- 90
問題1の解答
正解は「5」です。
問題1の解説
この問題は計算問題です。図の装置配置は「上の流れ(F1)は集じん装置を2回連続で通過する」「下の流れ(F2)は集じん装置を1回だけ通過する」という並列+一部直列の構造になっています。
したがって、総合集じん率93.0%は、3台を単純に直列にしたときの値ではなく、各ルートで取り切れずに“残った粉じん”を、流量比(=粉じん量の比)で重み付けして合算した結果として理解して逆算します。計算では「集じん率(取れる割合)」よりも「すり抜け率(残る割合)」を使うと、直列部分が掛け算で表せるため、手順が安定します。
なお、この考え方は、集じん・分離操作一般で用いる物質収支(マスバランス)と、直列機器での透過率(penetration)の乗算という工学的な基本原理に基づきます(環境工学・化学工学の標準的な扱いです)。
解答に至るまでのステップ
ステップ1 使う式を確認する
このステップでは、「直列の集じん装置は、集じん率を足すのではなく、すり抜けて残る割合が掛け算になる」という式の形を確認します。理由は、1台目で残った粉じんが、そのまま2台目に入るため、2台目が相手にする粉じんは「元の粉じん」ではなく「1台目通過後の残り」になるからです。そこで、集じん装置1台の集じん率を (90%なら0.90)と置き、1台通過後に残る割合(やさしい言葉で言うと“すり抜け率”)を
と定義します。参照すべき根拠としては、ここは法令や告示ではなく、集じん工学で一般に用いる定義(集じん率=1−透過率)と直列機器の扱い(透過率の乗算)に基づきます。
ステップ2 流量比と粉じん量の関係を整理する
このステップでは、問題文の条件「排ガスの分割によりばいじんも流量比に応じて分割される」を、計算に使える形に直します。理由は、合流後の総合集じん率は、上側と下側の出口粉じんを“同じ重さ”で平均するのではなく、流れる粉じん量の比で重み付けして合算しなければならないからです。
流量比が なので、全体を3とみなすと、上側()に入る粉じんは全体の 、下側()に入る粉じんは全体の です。ここでの根拠は、まさに問題文が明示している仮定(粉じんも流量比で分割)であり、物質収支(マスバランス)の前提条件になっています。
ステップ3 各ルートの“残る割合”を式で表す
このステップでは、図の装置配置を「残る割合 の何乗になるか」に変換します。理由は、直列は掛け算、並列合流は加算(重み付き)として一つの式にまとめるためです。上側ルートは集じん装置を2台直列で通るので、1台で残る割合が なら、2台通過後に残る割合は になります。一方、下側ルートは1台だけなので残る割合は のままです。さらに、上側に入る粉じんが全体の 、下側が なので、合流後に全体として残る粉じん割合は
と表せます。ここまでで「総合集じん率=93.0%」という条件を、計算できる一つの式に落とし込めたことが分かります。
ステップ4 総合集じん率93.0%と照らし合わせて逆算する
このステップでは、上で作った式を「残り7.0%」に等しいとして方程式を解き、最後に集じん率に戻します。理由は、与えられている93.0%は“取れた割合”であり、直列の整理に使っている は“残った割合”だからです。総合集じん率93.0%なら、残る粉じん割合は なので、
両辺に3を掛けて
二次方程式の解の公式より
なので、残る割合 として成り立つ(正の)解を採用し、
したがって より
つまり、集じん装置単体の集じん率は 90% です。選択肢では「5. 90」が一致します。
問題のポイント
この問題で誤答が生まれやすい最大の理由は、装置が複数あるときに「集じん率を足す」「2台直列だからηを2倍に近い感覚で扱う」といった、直感的だが誤った処理をしてしまう点です。
実際には、直列の本質は「2台目が相手にするのは、1台目で取り切れずに残った粉じんである」という流れの構造にあり、したがって足し算ではなく、“残る割合”の掛け算で扱うのが筋になります。この基本を押さえていないと、82〜88%のような“もっともらしい”選択肢に吸い寄せられます。
また、流量比1:2の意味を軽く見て「上側ルートと下側ルートを同じ重みで平均する」ことも典型的な落とし穴です。上側は装置が2台で強そうに見えますが、そもそも上側に流れる(=上側に入る粉じん)が全体の しかない以上、総合集じん率を決める支配的な要因は を占める下側ルートになります。ここを落とすと、「上側が強い=全体が強い」と誤解し、単体集じん率を過小評価して誤答に至ります。
本番での見分け方は、直列は“すり抜け率(残り)”を掛け算、並列合流は流量比で重み付けして足し算と決めて、必ず残り(1−集じん率)側で式を立てることです。












コメント