公害防止管理者の過去問|令和5年 ばいじん・粉じん特論 問2 問題と解説
問題2
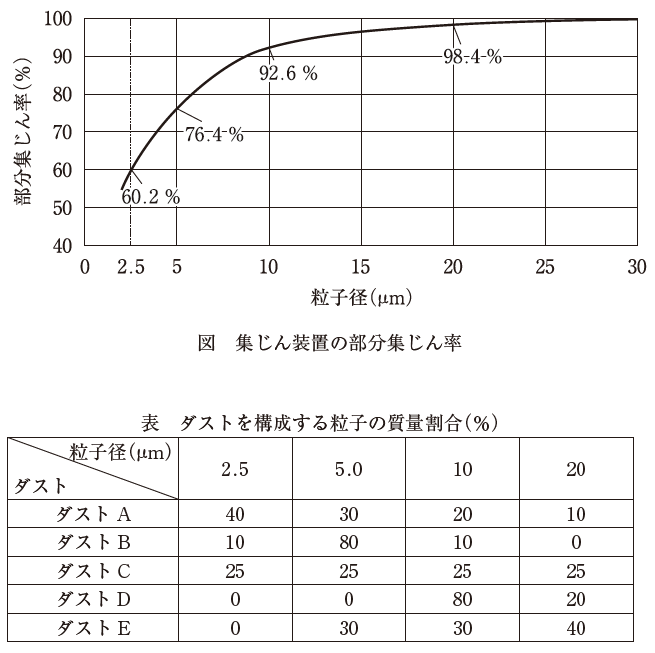
図に示す部分集じん率をもつ集じん装置で、4種類の粒子径の粒子を表に示す割合で混合したダストを含む排ガスを処理した。全集じん率(%)が最も高くなるダストはどれか。
- ダストA
- ダストB
- ダストC
- ダストD
- ダストE
問題2の解答
正解は「4」です。
問題2の解説
この問題は、図にある「粒子径ごとの捕集のしやすさ(部分集じん率)」と、表にある「粒子径ごとの混合割合(質量割合)」を使って、混合ダスト全体としてどれだけ捕まえられるか(全集じん率)を比べる計算問題です。
結論は、粒子径10 µmと20 µmの割合が大きいほど、図の部分集じん率が高い領域を多く使えるため全集じん率が上がります。表を見ると、その条件に最も当てはまるのがダストDなので、全集じん率が最大になります。
解答に至るまでのステップ
ステップ1 「何を求める問題か」と「使う計算ルール」を確認する
このステップでは、問題文の「全集じん率(%)が最も高くなるダスト」を見て、粒径ごとの部分集じん率を、粒径ごとの質量割合で重みづけして合計する問題だと確定します。理由は、ダストが複数粒径の混合で与えられており、装置の性能も粒径で変わるため、「粒径別の性能×粒径別の割合」を足し合わせないと全体性能が出ないからです。
このとき参照すべき学術的定義として、部分集じん率から総合集じん率(総合=全体)を求める考え方は「入口粉じんの質量分布関数で部分集じん率を加重して積分(離散なら加重平均)」として整理されています。
ステップ2 図から「粒子径ごとの部分集じん率」を読み取って表にする
このステップでは、図のカーブ上に明示されている数値を、そのまま粒子径ごとにメモします。理由は、ここを取り違えると以降の計算がすべて崩れるからです。読み取る値は次の4点です。
- 粒子径 2.5 µm:60.2%
- 粒子径 5.0 µm:76.4%
- 粒子径 10 µm:92.6%
- 粒子径 20 µm:98.4%
ステップ3 各ダストの「質量割合(%)」を抜き出し、加重平均で全集じん率を計算する
このステップでは、表の各ダストについて、粒径ごとの質量割合(%)を抜き出し、ステップ1のルールに従って「割合×部分集じん率」を足し合わせます。理由は、これが“混合物としてどれだけ捕集できたか”を表す最短の計算だからです。離散データなので、加重平均は次式で計算します(考え方は、部分集じん率を入口の質量分布で重みづけする総合集じん率の式と同じです)。
ここで、 は粒子径 の質量割合(%)、はその粒子径の部分集じん率(%)です。
実際に計算すると、
- ダストA:
- ダストB:
- ダストC:
- ダストD:
- ダストE:
ステップ4 計算結果を比較し、最大のものを選ぶ
このステップでは、ステップ3で出した5つの全集じん率を並べ、最も大きい値を選びます。理由は、設問が「最も高くなるダスト」を1つに定めているからです。比較すると最大は ダストD(93.76%) なので、正解は 4(ダストD) です。
問題のポイント
この問題は、図のカーブを「形」で眺めるのではなく、粒子径ごとの“数字”を読み取り、質量割合で加重して足すことができるかを確認しています。とくに「部分集じん率が高い粒径が多いダストほど、全体の集じん率が高い」というルールを、計算に落とせるかが核心です。
誤答選択肢が正しそうに見える理由は、たとえばダストEのように20 µmが多いと「98.4%が効くから最強」と感じやすい点にあります。しかしEは5 µmと10 µmもそれなりに含むため、Dのように10 µm(92.6%)に極端に寄せて全体を底上げするほどには伸びません。
受験者が陥りやすい具体的な思考の流れは、「カーブの右側はほぼ100%だから、20 µmが多いものだけを選べばよい」と早合点することです。実際には、各ダストは4粒径の混合なので、“高いところだけを見る”のではなく、“全部を割合で平均する”必要があります。
本番での見分け方は「表の割合(%)を小数に直し、図の部分集じん率(%)を掛けて足す。足し算の結果が最大のものを選ぶ」の1行に戻ることです。












コメント