公害防止管理者の過去問|令和3年 ばいじん・粉じん特論 問2 問題と解説
問題2
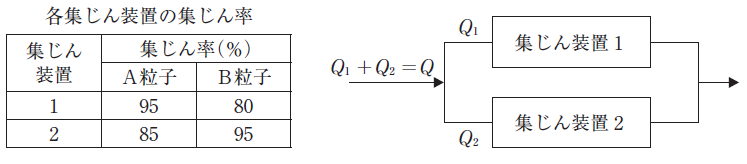
2種類の粒子(A、B)からなるダストを、並列に配置した2基の集じん装置により集じんする。
入口ガス中のA粒子とB粒子のダスト濃度比(A:B)は2:1で、各集じん装置のA粒子、B粒子に対する集じん率は表の通りである。
いま、ガス流量Q(m3/h)を、集じん装置1へのガス流量Q1(m3/h)と集じん装置2へのガス流量Q2(m3/h)に分割したとき、出口ダスト濃度が最も低くなるガスの分配比(Q1:Q2)はどれか。
ただし、ダストはガスの分割に伴い、その比率に等しく分割されるものとする。
- 1:0
- 2:1
- 1:1
- 1:2
- 0:1
問題2の解答
正解は「1」です。
問題2の解説
2種類の粒子AとBを含む粉じんを2基の並列集じん装置で捕集する場合、出口ダスト濃度を最小にするには、全ガス流量を性能の良い集じん装置にすべて通すのが最適です。
設問の条件では、集じん装置1のほうが粒子A・Bいずれに対しても効率が良いため、ガス分配比はQ₁:Q₂=1:0(全量を装置1に通す)となります。これは集じん効率の高い装置に全流量を通すことで全体の残留粉じん量が最小になるためです。
具体的には、入口粉じん濃度の組成A:B=2:1で、集じん装置1はA粒子95%除去・B粒子80%除去、装置2はA粒子90%除去・B粒子70%除去という効率条件(問題文中の表の値)とすると、計算上装置1通過後の残存粉じんは入口の約15%、装置2通過後は約17.5%になります。
装置1の方が残存率が低い(効率が高い)ため、すべてのガスを装置1に通した場合が最も出口濃度が低くなります。
したがって、他の選択肢(1:1や一部流量を装置2へ振り分ける)はいずれも効率面で劣ります。
問題を解くポイント
並列集じん装置への流量配分問題では、各装置の粉じん除去性能を比較し、性能の優れる装置に全量を通すのが基本となります。
特に、本問のように粉じんが均等に分割される(各装置に入る粉じんの組成比が同じ)場合、効率の差はそのまま出口濃度の差となるためです。
計算せずとも、「効率の良い装置にまとめて処理させる」という考え方で1:0または0:1の極端な配分が答えとなることに気付けます。












コメント