公害防止管理者の過去問｜令和4年 ばいじん・粉じん特論 問３  問題と解説

問題３

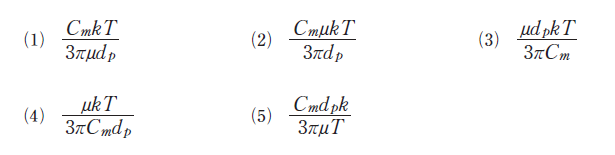
問題３の解答

正解は「１」です。

問題３の解説

解答に至るまでのステップ

ステップ1：ブラウン拡散係数の基本式

熱運動する微粒子の拡散係数（ブラウン運動拡散係数）は、流体力学におけるストークス–アインシュタインの式で表されます。
抵抗力がストークスの法則に従う球形粒子について、カニンガム補正係数を無視すると、$$D = \frac{k T}{3 \pi \mu d_{p}}$$D=3πμdp​kT​

となります。

ここで、

• $k$k：ボルツマン定数
• $T$T：絶対温度
• $\mu$μ：気体（流体）の粘度
• $d_{p}$dp​：粒子径

を表します。

ステップ2：カニンガム補正係数の考慮

実際の微小粒子では、粒子表面と気体分子の間にすべり（スリップ）が生じるため、ストークスの抵抗式に補正が必要になります。
この補正がカニンガム補正係数 $C_{m}$Cm​（文献によっては $C_{c}$Cc​ や $C_{s}$Cs​ と表記）です。

このとき、粒子に働く抵抗係数 $f_{\text{ric}}$fric​ は

$$f_{\text{ric}} = \frac{3 \pi \mu d_{p}}{C_{m}}$$

となります。

したがって、粒子に力 $F$F が作用したときの移動速度 $v$v は

$$v = \frac{F}{f_{\text{ric}}} = \frac{F \, C_{m}}{3 \pi \mu d_{p}}$$

と表されます。

ブラウン拡散では、この力 $F$F が熱ゆらぎに由来するエネルギー kTkTkT に対応すると考えられるため、拡散係数は

$$D = \frac{C_{m} \, k \, T}{3 \pi \mu d_{p}}$$

となります。

ステップ3：与えられた記号との照合

問題文では、

• $C_{m}$Cm​：カニンガム補正係数
• $k$k：ボルツマン定数
• $T$T：絶対温度
• $\mu$μ：ガス粘性率
• $d_{p}$dp​：粒子径

と定義されています。

したがって、求めるブラウン運動拡散係数は

$$\boxed{ D_{BM} = \frac{C_{m} \, k \, T}{3 \pi \mu d_{p}} }$$

となり、これが正解です。

問題を解くポイント

(1) ストークスの法則

半径 $d_{p}/2$dp​/2 の球形粒子が、低レイノルズ数条件で沈降・移動する場合の抵抗力は、ストークスの式により

$$F_{\text{drag}} = 3 \pi \mu d_{p} v$$

と表されます。
この考え方をブラウン運動に適用し、粒子が熱ゆらぎによって拡散移動する場合の拡散係数に結び付けたものが、ストークス–アインシュタインの式です。

(2) カニンガム補正係数

非常に小さな粒子では、粒子表面と気体分子との衝突によりすべり（スリップ）が生じ、流体抵抗が減少します。その結果、実効的な抵抗力はストークスの式で見積もられる値より小さくなります。

この効果を補正する係数が カニンガム補正係数 CmC_{m}Cm​ です。微粒子ほど $C_{m} > 1$Cm​>1 となり、抵抗が小さくなるため、結果として拡散係数は大きくなる方向に補正されます。式中に $C_{m}$Cm​ が掛かることで、ナノ粒子などでは補正なしの場合に比べて拡散しやすくなります。

(3) 式の次元確認

$kT$kT はエネルギーであり、単位は [J] です。一方、$3\pi\mu d_{p}$3πμdp​ は粒子の移動抵抗に対応する量です。

したがって、

$$\frac{kT}{3\pi\mu d_{p}}$$

は、拡散係数の次元である $[ \text{m}^2/\text{s} ]$[m2/s] を持つことになります。
各記号を問題文で定義された内容どおりに代入し、次元的に整合しているかを確認する習慣を持つことも、計算問題を正確に解くうえで重要です。