公害防止管理者の過去問｜令和5年 ばいじん・粉じん特論 問３  問題と解説

問題３

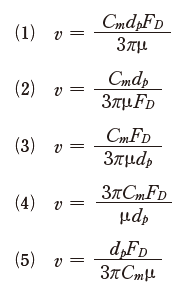
問題３の解答

正解は「３」です。

問題３の解説

解答に至るまでのステップ

ステップ1　出発点の式を「分数の形」として落ち着いて読む

ここで扱う出発点は、層流でのストークス抵抗（カニンガム補正込み）の形として与えられる次の式です。

$$F_D = \frac{3\pi \mu d_p v}{C_m}$$

この式は、「右辺は分数で、分子（上）に $3\pi \mu d_p v$、分母（下）に $C_m$​ がある」と読めば十分です。今回やることは、この式を “v=” の形に変形するだけです（中身の物理は一旦置いて、純粋な式変形として進めます）。

ステップ2　分母 $C_m$を消す（両辺に $C_m$を掛ける）

分数が出てきたときの定石は、分母を消すことです。右辺は「$C_m$で割っている」ので、両辺に $C_m$を掛ければ分母が消えます。

両辺に $C_m$を掛ける（式の両側に同じ操作をするのが“両辺”の意味です）：

$$F_D \times C_m = \frac{3\pi \mu d_p v}{C_m} \times C_m$$

右辺は「$/C_m$と $\times C_m$が打ち消し合う」ので、

$$C_m F_D = 3\pi \mu d_p v$$

ここまでで、もう分数がなくなり、だいぶ見やすくなります。

ステップ3　$v$以外を反対側へまとめる（両辺を $3\pi \mu d_p$ で割る）

いま欲しいのは $v$v だけが右辺または左辺に単独で残る形です。
現在は

$$C_m F_D = 3\pi \mu d_p v$$

右辺の $v$は、$(3\pi \mu d_p)$と「掛け算のかたまり」になっています。

両辺を $3\pi \mu d_p$で割る：

$$\frac{C_m F_D}{3\pi \mu d_p} = \frac{3\pi \mu d_p v}{3\pi \mu d_p}$$

右辺は分子・分母に同じ $(3\pi \mu d_p)$があるので打ち消えて、

$$\frac{C_m F_D}{3\pi \mu d_p} = v$$

通常は左に $v$v を置くので順番を入れ替えて（等号は左右を入れ替えても成り立ちます）、

$$v = \frac{C_m F_D}{3\pi \mu d_p}$$

これで「$v=\dots$v=…」の形が完成です。

ステップ4　完成した形を選択肢と一致判定する

最終形は

$$v = \frac{C_m F_D}{3\pi \mu d_p}$$

です。該当するのは （3） だけです。

問題のポイント

この問題は「物理を深く理解しているか」よりも、まずは 分数の形の式を、両辺操作で安全に変形できるかが勝負です。誤答は、$\mu$や $d_p$が分子に行ってしまったり、$C_m$が分母側に残ったりしており、“分母を消す→$v$の係数で割る”という手順を踏めば機械的に排除できます。