公害防止管理者の過去問|令和7年 ばいじん・粉じん特論 問3 問題と解説
問題3
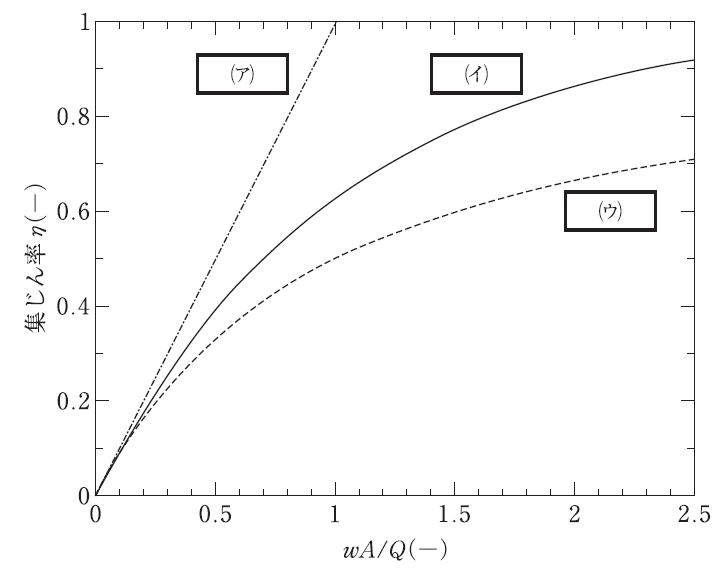
図は、流通形式集じん装置内の流動状態が異なる場合について、その集じん率ηとwA/Qの関係を装置内の流動状態ごとに示している。ア~ウの( )の中に挿入すべき語句の組合せとして、正しいものはどれか。
ただし、w:粒子の分離速度、A:装置の全集じん面積、Q:処理ガス流量、とする。
- 気流が乱流で、装置内すべてにおいてダスト濃度が均一
- 気流が層流
- 気流が乱流で、流れ方向断面においてダスト濃度が均一
| 選択肢 | ア | イ | ウ |
|---|---|---|---|
| (1) | A | B | C |
| (2) | A | C | B |
| (3) | B | C | A |
| (4) | C | A | B |
| (5) | C | B | A |
問題3の解答
正解は「1」です。
問題3の解説
この図は、集じん装置の「流れの混ざり方(流動状態)」の違いで、同じ wA/Q でも集じん率 が変わることを示しています。
- :粒子の分離速度(沈降・分離できる速さ)
- :全集じん面積
- :処理ガス流量
したがって、wA/Qは「装置が粒子を分離できる能力()に対して、ガスがどれだけ流れてくるか()」の比で、値が大きいほど集じんしやすい指標です。
解答に至るまでのステップ
ステップ1:図の“形”で3つの流動状態を見分けます。
図には3本の曲線があります。
- 原点から直線的に上がり、ある点で に達する線(左側の急な直線)
- 上に凸(だんだん頭打ち)で に近づく線(上の曲線)
- 同じく頭打ちだが、上の曲線より常に低い線(下の曲線)
ステップ2:層流(A)は“理想的に都合がよい”ので直線で表れます。
層流では流れが乱れにくく、粒子は比較的「まっすぐ」沈降できます。そのため、理想化すると集じん率は、(ただし最大1)のように wA/Qに比例して直線的に増え、wA/Q=1 で100%に到達する形になります。→ 図の 直線 が層流なので ア=A です。
ステップ3:乱流2ケース(BとC)は“混ざるほど不利”なので曲線になります。
乱流では混合が起こり、粒子が「せっかく沈みかけても流れに戻される」状況が増え、効率が落ちます。
- B:乱流で、流れ方向断面(各断面)では濃度が均一
→ 断面ごとには混ざるが、入口から出口へ進むにつれ濃度は下がる(“押し流されながら徐々に減る”タイプ)。
→ 一般に の形で、上側の曲線になります。 - C:乱流で、装置内すべてで濃度が均一(完全混合)
→ 装置全体が同じ濃度になりやすく、出口濃度も下がりにくい(“全体がずっと混ざってしまう”タイプ)。
→ 一般に の形で、Bより効率が低く、下側の曲線になります。
よって、上側の曲線=イ=B、下側の曲線=ウ=C。
結論:ア=A、イ=B、ウ=C → 選択肢1 です。
問題のポイント
- 層流(A):混ざりが少なく、理想化すると は 直線的に増え、条件次第で 100%到達しやすい。
- 乱流(B,C):混ざるほど粒子が再び流れに戻りやすく、は 頭打ち曲線になる。
- “完全混合(C)”が最も不利:装置全域が同濃度になり、出口濃度が下がりにくい → 同じ でも が一番低い。












コメント