公害防止管理者の過去問|令和6年 ばいじん・粉じん特論 問1 問題と解説
問題1
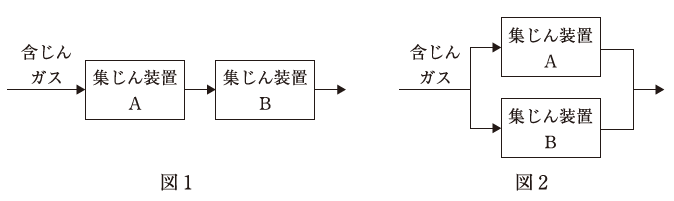
集じん率が92.6%の集じん装置Aと、集じん率が不明な集じん装置Bを図1のように直列につないだ際の総合集じん率は99.6%であった。
この二つの集じん装置を図2のように並列につなぎ変え、それぞれに1対1の流量比(ばいじんも流量比に応じて分割される)で含じんガスを流した場合、総合集じん率(%)はおよそいくらか。
なお、それぞれの集じん装置の性能は設置位置やつなぎ方により変化しないものとする。
- 89.6
- 92.1
- 93.6
- 96.1
- 97.6
問題1の解答
正解は「3」です。
問題1の解説
解答に至るまでのステップ
ステップ1 「集じん率」と「通過率(漏れ率)」に分けて考える(原理・原則)
集じん装置の性能は、次のどちらで考えてもよいのですが、直列・並列の計算では「通過率」(= 取り切れずに通り抜ける割合)で扱うとミスが減ります。
- 集じん率:(例:92.6% = 0.926)
- 通過率:(例:)
ここで重要なのは、直列は「通過が連続して起きる」ので通過率は掛け算、並列は「出口で混ざる」ので通過率は加重平均になる、という原理です。
ステップ2 図1(直列)から、装置Bの集じん率を逆算する
直列接続の総合通過率 は
与えられた条件を数値化します。
- 装置Aの集じん率: → 通過率
- 直列時の総合集じん率:→ 総合通過率
よって
つまり、装置Bの集じん率は約 94.6%です。
ステップ3 図2(並列・流量比1:1)で総合集じん率を求める
問題文に「流量比1:1(ばいじんも流量比に応じて分割)」とあります。これは、各枝に入る含じんガスの濃度(= ばいじん量/ガス量)が同じになる、という意味です(半分の流量に、ばいじんも半分ずつ入るため)。
並列では、出口で2つの流れが混ざるので、総合通過率 は「通過率の加重平均」になり、流量が1:1なら単純平均です。
したがって総合集じん率は
よって正解は 93.6%(選択肢3)です。
問題のポイント
- 直列は「通過率の掛け算」:(取り逃しが連続して減る)
- 並列は「通過率の加重平均」:
- 今回は流量比1:1、かつ「ばいじんも流量比で分割」なので濃度が等しくなり、並列総合は
→ 集じん率は約93.6%となります。












コメント